前言

序列标注（Sequence Labeling）是机器学习的一大分支，特别在NLP领域用途更广，因为人类语言是由一系列的顺序符号组成，本身就是一个文字序列。序列标注可以应用 在分词、词性标志、实体识别等领域。

序列标注有多种算法，常见的HMM（隐马尔科夫）、CRF（条件随机场）。这两个模型（包括MEMM）有非常多的相似之处和细微的差别，网上的大量文章对此的描述多是通过 大量的文字和一些简单的公式或图片来说明，细节的部分表述不够清楚。要精确的理解他们的差异，需要从算法的数学理论出发。

下面详细介绍HMM模型。

符号定义

为了便于理解，下面将结合一个具体的序列标注应用场景–词性标注，来进行说明。

1. $X$：变量，表示一个句子（一个字序列）
2. $X^n$：表示集合中的第n个句子，由K个字组成，$X_1^{(n)},X_2^{(n)},…,X_k^{(n)}$
3. $X_k^n$：表示第n个句子的第k个字，字构成句子
4. $Y$：变量，表示一个词性序列
5. $Y^n$：表示集合中的第n个句子对应的词性序列，由K个词性组成，$Y_1^{(n)},Y_2^{(n)},…,Y_k^{(n)}$
6. $Y_k^n$：表示第n个句子的第k个字对应的词性，所有词性构成一个词性序列
7. $D$：表示整个数据集，包括所有句子和词性序列，${{X^{(n)},Y^{(n)}}}_{n=1}^N$

建模

对序列标注（sequence labeling）模型进行讲解，通常会使用隐藏序列和观察序列，理解起来有点抽象，为了更好的结合实际案例来理解，本文采用词性标注的应用案例。那么，对序列标注模型的基本建模思路就是：
定义一个次序列（也就是一个句子）$X=X_1,X_2,…,X_k$和对应的词性序列$Y=Y_1,Y_2,…,Y_k$，通过$X,Y$的联合概率进行建模:

$$P(X,Y)=P(Y)P(X|Y),formula\ (1)$$

其中，

$$P(Y)=P(Y_1)*P(Y_2|Y_1)*P(Y_3|Y_2Y_1)...*P(Y_K|Y_{K-1}...Y_1))=P(Y_1)\prod_{i=2}^K{P(Y_i|Y_{i-1}...Y{1})}$$

这里涉及到多种概率，假设X=我想学习机器学习，那么需要考虑到P(我)、P(想|我)、P(学|我想)、…、P(习|我想学习机器学)等一系列的概率。这样会导致概率的稀疏性，模型复杂度也比较高。那么我们需要引入一些假设，通过这些假设来简化模型（简单的模型不一定比复杂的模型效果差，越简单的模型，一般泛化能力更好，在简单场景和小数据上表现也不差）。

这里引入HMM的第一个假设，$P(Y_i|Y_{i-1}…Y_1)=P(Y_i|Y_{i-1})$，即词性序列$Y_i$之间的一阶依赖关系，叫做一阶马尔科夫性质。更具体的说，就是当前词的词性只依赖于上一个词的词性，和其他词的词性无关。这样：

$$P(Y)=P(Y_1)\prod_{i=2}^K{P(Y_i|Y_{i-1})}$$

为了让上面的公式看起来更加简洁，引入$Y_0$，满足$P(Y_1|Y_0)=P(Y_1)$，那么上面的公式写为：

$$P(Y)=\prod_{i=1}^K{P(Y_i|Y_{i-1})}$$

对于$P(Y|X)$，引入HMM的第二个假设：$X_i$只和$Y_i$相关（这里隐含的意思是，除了$Y_i$之外，$X_i$和其他特征或状态都是无关的，比如，$X_i$和$X_{i+1}$是无关的。在后面的MEMM和CRF模型中，能看到他们和HMM在独立性假设上的差异），那么：

$$P(X|Y)=\prod_{i=1}^K{P(X_i|Y_kY_{k-1}...Y_1)}$$ $$=\prod_{i=1}^K{P(X_i|Y_i)}$$

这样，HMM在两个假设的前提下，简化为：

$$P(X,Y)=\prod_{i=1}^K{P(Y_i|Y_{i-1})}\prod_{i=1}^K{P(X_i|Y_i)}$$

对于所有的N个样本数据，HMM的最大似然目标是需要所有样本的$P(X,Y)$的概率乘积最大。这是一种机器学习领应用非常多的最大似然参数估计方法，假设每个样本$(X,Y)$之间是相互独立的，那么N个样本的概率分布就是每个样本的概率分布的乘积，通过最大化这个概率乘积，能得到全局最优的概率分布参数：

$$\prod_{n=1}^N{P(X^{(n)},Y^{(n)})}=\prod_{n=1}^N({\prod_{i=1}^K{P(Y_i^{(n)}|Y_{i-1}^{(n)})}\prod_{i=1}^K{P(X_i^{(n)}|Y_i^{(n)})}})$$

为了下面书写更简洁，符号做下重新定义：$t_{i,j}^{(n)}=P(Y_i^{(n)}|Y_j^{(n)})$，$e_{i,j}^{(n)}=P(X_i^{(n)}|Y_j^{(n)})$。

下面开始构造数学化的目标函数。上面的推导过程其实隐含了一些条件：

1. $t_{i,j}$是一个概率分布，所以：$0<=t_{i,j}<=1$，$\sum_{i\in{I}}{t_{i,j}=1}$
2. $e_{i,j}$也是一个概率分布，所以：$0<=e_{i,j}=1$，$\sum_{i\in{I}}{e_{i,j}=1}$

这样，HMM的目标函数表示为：

$$\mathop{\arg\max}_{t,e}{\prod_{n=1}^N({\prod_{i=1}^K{t_{i,i-1}^{(n)}e_{i,i}^{(n)}}})}$$ $$st.\ 0<=t_{i,j}<=1,\ \sum_{i\in{I}}{t_{i,j}=1}$$ $$0<=e_{i,j}=1,\ \sum_{i\in{I}}{e_{i,j}=1}$$

参数估计

Inference

HMM的预测，目的是找到一个最优的词性序列$Y$，使得联合概率$P(X,Y)$最大化。最朴素直接的方法就是枚举出所有的$Y$序列，假设词性序列长度为K，词性的状态集合大小为S，那么$Y$的可能组合个数为K*S。计算出所有$(X,Y)$的最大值。

这种朴素的方法性能会比较慢，做了非常多的重复计算。需要使用动态规划的方法进行最优Y序列的推导（叫做维特比算法）。

Inference的目标是找到最优的：

$$P(X,Y)=\prod_{i=1}^K{t_{i,i-1}^{(n)}e_{i,i}^{(n)}}$$

$P(X,Y)$其实就是一系列的$t,e$概率的乘积。用一个有向图来更形象的表示这个概率，用图论的一个经典解法就能找到最优的Y。这个有向图总共有K个时刻（序列长度），每个时刻有S个节点（词性的标签集合大小），代表在t这个序列位置的词性标签，加上开始和结束两个节点，构成一个有向图，图中的每条边的权重代表概率$t_{i,i-1}e_{i,i}$。

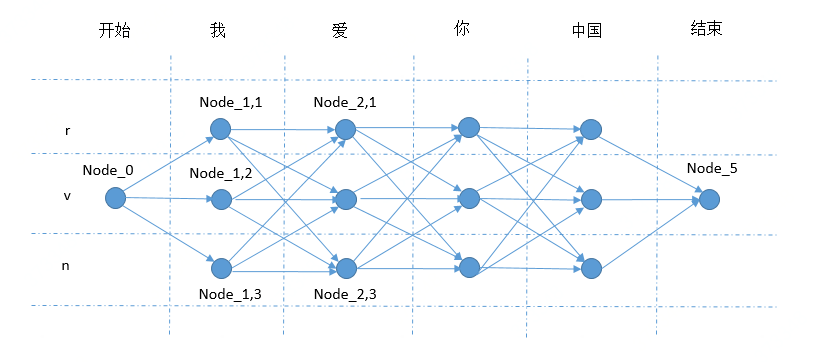
用上图的词性标注例子来举例，序列长度K=4，词性标签集合大小S=3（名词n，动词v，代词r），$Node_{1,1}$表示’我’对应的词性n，$Node_{1,2}$表示’我’对应的词性v，$Node_{1,3}$表示’我’对应的词性r，$Node_{2,1}$表示’爱’对应的词性n，$Node_{2,2}$表示’爱’对应的词性v，$Node_{2,3}$表示’爱’对应的词性r，以此类推。用$Edge_{(1,1)->(2,1)}$表示$Node_{1,1}$到$Node_{2,1}$的边，边上的权重为$P(爱|v)P(v|r)$

那么找到概率最大的$P(X,Y)$就转化为从图中的开始节点到结束节点，找到一条最优的路径，这个最优的路径的每个边的权重的乘积是最大的。恰好，图论的单源最短路径算法就是用来解决这个问题的，其中最经典的就是动态规划。

（关于这里的动态规划，简单说，就是t时刻的最优值是可以通过t-1时刻的最优值计算得来，相对于朴素的深度搜索方法，能避免重复搜索，这里重点讲HMM，动态规划翻一下“算法导论”会有比较详细的解答）

详细讲下这里HMM的Inference计算过程，便于理解，图中的纵轴方向表示词，横轴方向表示词性，我们的目的就是要找到从左到右的一条最优路径：

1. $Node_{1,1}=Edge_{(0)->(1,1)}$，其中$Edge_{(0)->(1,1)}=P(我|r)P(r|开始)$
2. $Node_{1,2}=Edge_{(0)->(1,2)}$，其中$Edge_{(0)->(1,2)}=P(我|v)P(v|开始)$
3. $Node_{1,3}=Edge_{(0)->(1,3)}$，其中$Edge_{(0)->(1,2)}=P(我|v)P(v|开始)$
4. $Node_{2,1}=MAX(Node_{1,1}*Edge_{(1,1)->(2,1)},\ Node_{1,2}*Edge_{(1,2)->(2,1)},$ $\ Node_{1,3}*Edge_{(1,3)->(2,1)})$，其中$Edge_{(1,1)->(2,1)}=P(爱|r)P(r|r)$，$Edge_{(1,2)->(2,1)}=P(爱|r)P(r|v)$，$Edge_{(1,3)->(2,1)}=P(爱|r)P(r|n)$

……

直到计算到$Node_{5}$，找到最大一个值，就是最优的$P(X,Y)$，对应的路径采用一些回溯的方法即可找到，这里不再赘述。比如在这个例子中，我们找到的路径就是：$Node_{0},Node_{1,1},Node_{2,2},Node_{3,1},Node_{4,3},Node_{5}$，表示词性：我(r)爱(v)你(r)中国(n)。

---

• Next
  SVM进阶

---