前言

网上介绍SVM理论的文章非常的多，自己也看过不少，大部分存在一个比较大的问题，很多理论推导部分一笔带过，引入了非常多的中间结论，对于为什么可以引用这些结论，这些结论从何而来，没有详细的说明，导致整个推导过程存在不少断层，不够完整，本文希望完成一个比较完整、清晰、严谨的推导过程。

符号说明

1.’大写字母’表示向量，比如$X$表示一个$t$维向量[$X_1,X_2,…,X_t$]。

2.’大写字母+下标数字’表示n维向量中的一个维度的数据，比如$W_1$表示向量X中的第一个维度

3.’大写字母+(上标数字)’表示某一个具体的向量，比如$W^{(i)}$表示$t$维向量[$W^{(i)}_1,W^{(i)}_2,…,W^{(i)}_t$]

4.’小写字母’表示常量，比如$b$

5.’小写字母+(上标数字)’表示某一个具体的常量，比如$b^{(i)}$

1和3的区别类似随机变量和某一个具体样例之间的关系

目标函数

考虑最基本的二分类问题。

我们把所有正负样本映射到多维空间的点，考虑最简单的一种情况：所有的正负样本是可以被一个线性超平面完全正确的区分开来（即，所有的正样本都是超平面的上方，所有的负样本都是超平面的下方）

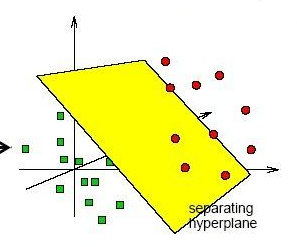
将此转换成数学量化的目标:

$$\arg\max_{W,b}margin(W,b)\,st.\ every\ y^{(n)}(W^TX^{(n)}+b)>0$$

其中，根据点到平面的距离公式：

$$d=\frac{|W^TX^{(n)}+b|}{\sqrt{W_1^2+W_2^2+...+W_t^2}}=\frac{y^{(n)}(W^TX^{(n)}+b)}{||W||}$$

因为$y_n$取值为+1或-1，通过引入$y_n$可以把分子的绝对值去掉，这样有

$$margin(W,b)=\min_{n=0...N}(\frac{1}{||W||}y^{(n)}(W^TX^{(n)}+b))$$

表示所有样本点中到某一个固定平面（W,b）的最小距离，$x^{(n)}$表示第n个点的特征向量，$y^{(n)}$表示第n个点的label（+1和-1），b表示平面的上下位移（否则平面就只能过原点）。目标函数是希望：在保证超平面能将所有正负样本点完全分开的情况下，最大化点到平面的最小距离（更详细的解释这句话的意思就是：对于某一个固定的平面，找到所有点到这个平面的最小距离d，我们希望找到最优的一个平面，它对应的距离L是最大的）。

原问题求解

对于上面的目标函数，可以进一步的简化对任意一个待选平面($W^{(i)},b^{(i)}$)，设所有样本点到其平面的最小距离$d=\frac{K}{||W^{(i)}||}$，那么原目标函数等价变换为

$$\arg\max_{W^{(i)},b^{(i)}}{\frac{K}{||W^{(i)}||}},\ st.\ every\ y^{(n)}({W^{i}}^TX^{(n)}+b^{(i)})$$

其中，最小距离的点($X^{(s)},y^{(s)}$)满足$y_{(s)}({W^{(i)}}^TX^{(s)}+b^{(i)})=K$

引入一个新的变量$U^{(i)}$和$c{(i)}$，令$W^{(i)}=KU^{(i)}$,$b^{(i)}=Kc^{(i)}$，上面的目标函数变为：

$$\arg\max_{U^{(i)},c^{(i)}}\frac{K}{||KU^{(i)}||}\ st.\ every\ y^{(n)}(K{U^{(i)}}^TX^{(n)}+Kc^{(i)})>=K$$

等价于

$\arg\max_{U^{(i)},c^{(i)}}\frac{1}{||U^{(i)}||}\ st.\ every\ y^{(n)}({U^{(i)}}^TX^{(n)}+c^{(i)})>=1,\ formula(1.1)$

也就是将原来的($W^{(i)},b^{(i)}$)经过$K$倍缩放变换到($U^{(i)},c^{(i)}$)进行求解，虽然得到的数值$W^{(i)}$,$U^{(i)}$,$b^{(i)}$,$c^{(i)}$不一样，但是满足$W^{(i)}=KU^{(i)}$,$b^{(i)}=Kc^{(i)}$关系，平面的系数变为原来的K倍之后还原来的平面（比如，$x^{(1)}+x^{(2)}+1=0$和$2x^{(1)}+2x^{(2)}+2=0$是两个完全一样的平面）。

注意，以上只是针对一个固定的平面($W^{(i)},b^{(i)}$)的推导过程。同样，对于其他的任意一个平面，都能转换成formula(1.1)的形式，不过是其中的$K$不一样（这点也非常重要）。所以我们可以得到结论formula(1.1)的最优解是和原公式的最优解是存在$K$倍关系的（注意$K$是一个变量，不用的平面$K$值不同）。这里特别的是，平面的系数经过$K$倍缩放之后，还是原来的平面（注意是$x,y$都同时缩放），所以得到的$U$就是我们想要找到的$W$。

这样，整体的目标函数写为：

$\arg\max_{W,b}\frac{1}{||W||}\ st.\ every\ y^{(n)}(W^TX^{(n)}+b)>=1$
等价于：

$\arg\min_{W,b}\frac{1}{2}W_TW\ st.\ every\ y^{(n)}(W^TX^{(n)}+b)>=1,\ formula(1.2)$

注意，这里为了方便书写，$W$,$b$是指经过$K$倍变换后的新变量（也就是上面的$U$,$c$）
这个目标函数已经是标准的Quadratic Programming（二次规划）问题，使用二次规划工具即可以求解得到最优解。Quadratic Programming问题参看https://en.wikipedia.org/wiki/Quadratic_programming

Hard-Margin Dual SVM

对formula(1.2)，可以使用朗格朗日乘子法进行求解，定义朗格朗日函数：

$$L(W,b,\alpha)=\frac{1}{2}W_TW+\sum_{n=1}^{N}(\alpha_n(1-y_n(W^TX_n+b))),\ formula(1.3)$$

其中，我们约束

$$\alpha^{(n)}>=0,1-y_n(W^TX^{(n)}+b)<=0,\ formula(1.4)$$

设$f(W,b)=\frac{1}{2}W^TW,\ formula(1.5)$

那么对于任意一个$W,b$,存在关系：$f(W,b)>=L(W,b,\alpha)$。显然，如下公式也成立：

$$\min_{W,b}{f(W,b)}>=\min_{W,b}{L(W,b,\alpha)}$$

其中$\min_{W,b}{f(W,b)}$表示所有$f(W,b)$中的最小值（即，处处都有$f<L$，两个函数的最小值必定也存在关系$\min_{}{f}>=\min_{}{L}$）

进一步往下推导：

$$\min_{W,b}f(W,b)>=\min_{W,b}L(W,b,\alpha)$$ $$=\min_{W,b}{(\frac{1}{2}W^TW+\sum_{n=1}^{N}{\alpha^{(n)}(1-y^{(n)}(W^TX^{(n)}+b))})}$$ $$=\min_{W,b}(\sum_{t=1}^T(\frac{1}{2}{W_t}^2)+\sum_{n=1}^N(\alpha^{(n)}(1-y^{(n)}(\sum_{t=1}^T(W_t{X_t^{(n)}})+b)))$$ $$=\min_{W,b}(\sum_{t=2}^T(\frac{1}{2}{W_t}^2)+\sum_{n=1}^N\alpha^{(n)}-\sum_{n=1}^N(\alpha^{(n)}y^{(n)}\sum_{t=1}^T(W_tX_t^{(n)})-\sum_{n=1}^N(\alpha^{(n)}y^{(n)}+b))$$ $$=\min_{W,b}(\sum_{t=1}^T(\frac{1}{2}{W_i}^2)-\sum_{t=1}^T(W_i\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)}))-\sum_{n=1}^N(\alpha^{(n)}y^{(n)}b)+\sum_{n=1}^N(\alpha^{(n)}))$$ $$=\min_{W,b}(\sum_{t=1}^T(\frac{1}{2}{(W_t-\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)}))}^2)-\frac{1}{2}\sum_{t=1}^T{(\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)}))}^2-\sum_{n=1}^N(\alpha^{(n)}y^{(n)}b)+\sum_{n=1}^N(\alpha^{(n)}))$$ $formula(1.6)$

要使得$formula(1.6)$最小，首先必须：对于所有的$t$,有$W_t-\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)})=0$，即：

$$W_i=\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)}),\ formula(1.5)$$

$formula(1.6)$接着往下推导：

$$-\frac{1}{2}\sum_{i=t}^T{(\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)}))}^2-\min_{W,b}\sum_{n=1}^N(\alpha^{(n)}y^{(n)}b)+\sum_{n=1}^N\alpha^{(n)},\ formula(1.6)$$

设$h(\alpha,b)=formula(1.7)$，那么把$h(\alpha,b)$叫做原问题的弱对偶问题，即：

$$\min_{W,b}f(W,b)>=h(\alpha,b)$$

进一步，由于$b$也是原问题需要优化的一个参数，为了排除$b$的影响，再增加一个充分条件：

$$\sum_{n=1}^N(\alpha^{(n)}y^{(n)}b)=0\ <==>\ \sum_{n=1}^N(\alpha^{(n)}y^{(n)})=0$$

则：

$$h(\alpha,b)=-\frac{1}{2}\sum_{t=1}^T{(\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_t^{(n)}))}^2+\sum_{n=1}^N\alpha^{(n)}$$ $$=-\frac{1}{2}\sum_{t=1}^T{(\sum_{m=1}^N\sum_{n=1}^N(\alpha^{(n)}\alpha^{(m)}y^{(n)}y^{(m)}X_i^{(n)}X_i^{(m)}))}+\sum_{n=1}^N\alpha^{(n)}$$ $$=-\frac{1}{2}\sum_{m=1}^N\sum_{n=1}^N(\alpha^{(n)}\alpha^{(m)}y^{(n)}y^{(m)}{X^{(n)}}^TX^{(m)})+\sum_{n=1}^N\alpha^{(n)}$$

（注意上面的公式中，部分T表示特征维度，部分T表示向量的转置，不要混淆）

由于$h(\alpha,b)$中已经没有$b$参数，我们换一个表达式$g(\alpha)=h(\alpha,b)$

那么，可以通过最大化$g(\alpha)$来逼近$f(W,b)$的最小值。换个角度理解，我们是想要找到$\alpha^*=\arg\max_{\alpha}g(\alpha)$，这时的$g(\alpha^*)$是最接近$f(W^*,b^*)$的（$f(W^*,b^*)=\min_{W,b}f(W,b)$）

借助一个图来说明就是（注意图中的$f^*=\min_{W,b}f(W,b)$，而不是$\arg\min_{W,b}f(W,b)$）：

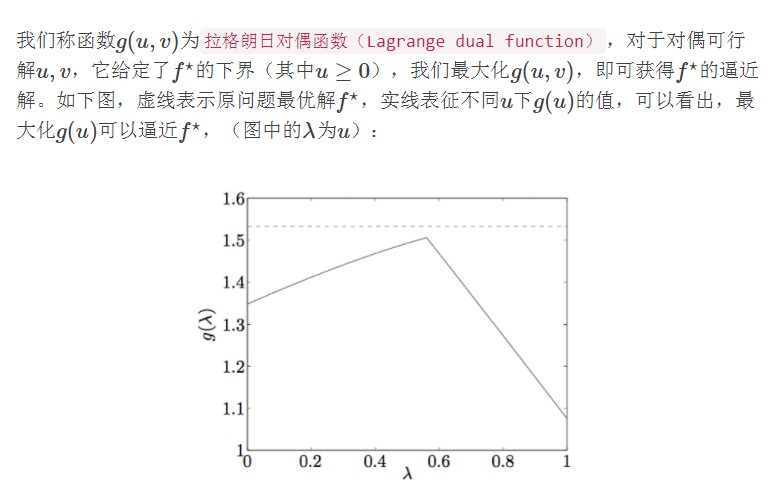
截止目前，在满足一系列充分条件的前提下（参看前面推导过程中做的所有假设），我们得到：

$$\min_{W,b}f(W,b)>=\min_{W,b}L(W,b)=g(\alpha)$$

根据定义$formula(1.3),formula(1.4)$，再增加一个充分条件：

$$\sum_{n=1}^N(\alpha^{*(n)}(1-y^{(n)}(W^{*T}X^{(n)}+b^*)))=0,\ formula(1.8)$$

这时：$f(W^*,b^*)=L(W^*,b^*,\alpha^*)=g(\alpha^*)$

其中，$(W^*,b^*)=\arg\min_{W,b}f(W,b)$，$\alpha^*=\arg\max_\alpha(\alpha^*),\ formula(1.9)$

即在满足这一系列充分条件的前提下，弱对偶问题成为强对偶问题。

那么’这一系列的充分条件’是什么呢，回顾我们之前的推导过程，把所有的假设列出来，即是强对偶问题成立的充分条件：

$\begin{pmatrix} \alpha^{(n)}>=0 \\\\ 1-y_n(W^TX^{(n)}+b)<=0 \\\\ W_i=\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_i^{(n)}) \\\\ \sum_{n=1}^N(\alpha^{(n)}y^{(n)})=0 \\\\ \sum_{n=1}^N(\alpha^{*(n)}(1-y^{(n)}(W^{*T}X^{(n)}+b^*)))=0 \end{pmatrix}$

对于上面的第5个条件，由于1,2条件的存在，所有求和公式里的每一项都必须为0，则充分条件进一步表示为：

$\begin{pmatrix} \alpha^{(n)}>=0 \\\\ 1-y_n(W^TX^{(n)}+b)<=0 \\\\ W_i=\sum_{n=1}^N(\alpha^{(n)}y^{(n)}X_i^{(n)}) \\\\ \sum_{n=1}^N(\alpha^{(n)}y^{(n)})=0 \\\\ \alpha^{*(n)}(1-y^{(n)}(W^{*T}X^{(n)}+b^*))=0 \end{pmatrix}$

这5个条件就是KKT条件。在上面的推导过程中，我们证明了KKT是强对偶成立的充分条件，事实上，它也是必要条件（这里没有再做证明）。

总结我们的推导过程：即在满足上面的充分条件的前提下，能够使得强对偶情况成立，那么可以通过求解$\max_{\alpha}g(\alpha)$来得到原问题的其中一个最优解（注意这里只是原问题的其中一个最优解，如果对于原问题，有且仅有一个最优解，那么对偶问题求得的解也一定是原问题的唯一最优解）。

Dual Problem 求解

按照上一节dual-problem的推导过程，整理dual-problem的求解过程如下。

找到对偶问题的最优解$\alpha^*$：

$$\arg\max_{\alpha}g(\alpha),\ st.\ to\ \alpha^{(n)}>=0,\sum_{n=1}^N(\alpha^{(n)}y^{(n)})=0$$

这个问题仍然是一个Quadratic Programming问题，可以通过QP工具直接求解。

得到最优的$\alpha^*$之后，利用KKT条件中的第3个条件，可以计算得到$W^*$。利用KKT条件中的第5个条件，当$\alpha^*=0$时，可以得到$b^*$，这样就得到了原问题需要求解的最优解$(W^*,b^*)$。

Why dual problem

要了解这个问题，需要稍微理解下Quadratic Programming。引用台湾大学的机器学习资料，原问题和对偶问题的QP求解方法如下：

其中，左上角表示原问题的目标函数，右上角表示通用的QP问题，通过定义变量$u,Q,p,a_n^T,c_n$，将原问题对应到通用QP问题，就可以直接求解了。

这里关键的是$Q$矩阵，$Q$矩阵中的$d$表示的是$W$的维度，也就是特征向量的维度，$Q$是一个$2dX2d$的矩阵。在实际应用中，$d$可能会是非常大的一个数字，比如做文本分类，文本特征向量一般都是非常稀疏的向量，如果$d$是30000维，那么$Q$的空间占用是30000X30000（>3GB），相当的大。

考虑对偶问题

$Q$的空间是和sample的数量$N$相关的，这是不同于原问题的qp问题的，两者在内存占用上不同。

另一方面。通过核函数，可以把原问题的特征空间$X$升维到高维空间（同样的$W$也要升维到高维空间），也可以是无限维的空间（下面核函数的时候会再讲）。如果是无限维的空间，通过原问题求解的方式，$Q$是无限维的，根本不可能求解。这时对偶问题就体现出巨大的优势，和特征向量维度$d$没有关系，只和样本数量$N$有关，这样通过原问题无法求解的问题，在对偶问题下巧妙的解决了！

注意，上面图片中$q^{n,m}$的计算有一部分是${Z^{(n)}}^TZ^{(m)}$（$Z^{(n)}$表示$X^{(n)}$转换为高维空间后新的向量），细心的人可能已经想到，这里的计算复杂度也是跟特征的维度相关的，所以对偶问题还是和特征维度相关的。这就涉及到kernel function了，在后面的kernel funcition里面会讲到，我们可以巧妙的避免这个问题

总结两种方法的特点如下：

原问题：

适用低维特征向量
核函数无限维特征的情况下无法求解

对偶问题：

适用样本数量少
可以用于核函数无限维特征的情况

SVM进阶

SVM-advanced

前言